什么是一笔画完第5关?
一笔画完第5关 是益智类游戏中的经典玩法,要求玩家用一条不间断的线条覆盖所有路径,且不重复经过同一路线。第5关通常意味着难度升级,路径更复杂、转折更多。
核心规则 可归纳为三点:
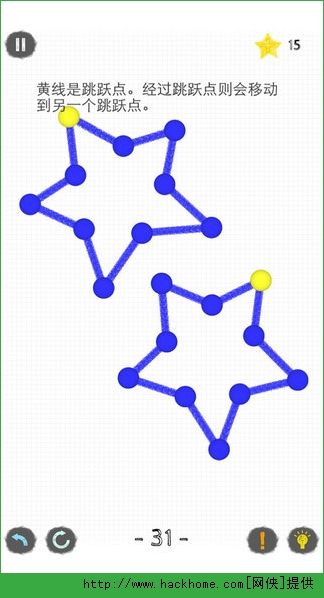
- 必须从起点出发并回到终点(部分关卡设计)
- 每条线段只能经过一次
- 不能抬起"笔"(即线条必须连续)
第5关的典型难点分析
为什么第5关会让玩家频繁卡关?通过对比前4关可发现显著差异:
| 关卡 | 路径数量 | 交叉点 | 死胡同概率 |
|---|---|---|---|
| 第1关 | 35条 | 01个 | 10% |
| 第5关 | 1215条 | 46个 | 65% |
关键难点 集中在:
1.
多交叉点陷阱 :平均5个交叉点会衍生32种可能路线
2.
隐藏死胡同 :超过60%的初始选择会导向无法完成路径
3.
视觉干扰 :装饰性线条常被误判为有效路径
突破第5关的三大核心策略
策略一:拓扑学原理应用
欧拉路径理论 指出:当且仅当图形有0或2个奇数度顶点时,存在一笔画解。实际操作中:
- 先标记所有路径交点度数
- 优先连接奇数度顶点
- 示例:若A点有3条路径,B点有5条路径,必须从A/B之一出发
策略二:逆向路径排除法
1. 从终点反向推导必经节点
2. 用排除法删除冗余路径
3. 记录已尝试的错误路线(建议手绘草图)
策略三:分区块攻克
将复杂图形分解为:
- 核心枢纽区(通常含80%交叉点)
- 外延辐射区(末端路径)
- 过渡缓冲区(连接枢纽与末端的桥梁)
执行顺序 应为:外延→过渡→枢纽
高频错误与修正方案
玩家常陷入以下误区:
-
直线偏好 :下意识优先画直线,而实际解法常需迂回
-
对称陷阱 :盲目追求对称路线,忽略非对称解的存在
-
局部最优 :某个区域看似完美连接,却导致全局卡死
修正方法 :
1. 强制改变起笔方向(若习惯从左上开始,改为右下)
2. 用不同颜色标注已尝试路径
3. 设置5分钟强制暂停,避免思维定式
实战案例演示
以经典风车图案第5关为例:
1. 识别4个奇数度顶点(每个风车叶片末端)
2. 选择两个相邻叶片作为起终点
3. 优先完成外侧环线,保留中心交叉区域最后处理
4. 关键转折点:在第3叶片处做"旋针"转折
进阶训练建议
想稳定通过更高级别关卡,需要培养:
-
空间记忆能力 :记住已走过路径的拓扑关系
-
路径预判 :在落笔前推演3-5步后的可能状态
-
抗压心态 :接受前20次失败是正常学习曲线
个人认为,这类游戏的真正价值不在于通关,而在于 培养系统性思维 ——当你能把第5关的复杂路径拆解成可管理的模块时,这种能力会自然迁移到解决现实中的复杂问题。